This article describes the LuciadLightspeed support for map projections. It does not describe the theory of map projections. For a theoretical background refer to the literature as given in Literature on map projections.
Using an ILcdProjection describes the interface ILcdProjection, which forms the basis.
Extensions of ILcdProjection describes the main extensions of this interface, and Main implementations of ILcdProjection describes the main implementations of these extensions.
Using an ILcdProjection
An ILcdProjection is a transformation of geographically referenced data into a planar (flat) representation of the earth’s surface and conversely.
In LuciadLightspeed a planar coordinate representation is denoted as world coordinates. The geographically referenced data are expressed as geodetic lon-lat-height coordinates with respect to an ILcdGeodeticDatum. The planar representation is expressed in a Cartesian two-dimensional coordinate system using X and Y coordinates. The planar
representation is usually used for visualization or for the definition of a grid reference system.
The main methods of the interface ILcdProjection concern the transformation of geographically referenced data to the planar representation and the other way around. The approximation
of the earth can either be with a sphere or an ellipsoid.
Program: Transformations between geodetic and world coordinates shows how to transform geodetic lon-lat-height coordinates based on an ILcdEllipsoid (called ellipsoid) to planar XY coordinates which are represented by ILcd2DEditablePoint objects. For the inverse transformation of projections that take the ellipsoidal height into account, the assumption is that
this height is already available within the side effect parameter LLHP2 (of type ILcd3DEditablePoint), such that only the longitude and latitude have to be determined.
projection.lonlatheight2worldOnEllipsoidSFCT(LLHP, ellipsoid, XY);
projection.world2lonlatOnEllipsoidSFCT(XY, ellipsoid, LLHP2);
projection.lonlatheight2worldOnSphereSFCT(LLHP, radius, XY);
projection.world2lonlatOnSphereSFCT(XY, radius, LLHP2);In general, an ILcdProjection projects only a part of the world to a plane. If a coordinate is passed to the methods shown in Program: Transformations between geodetic and world coordinates, and that coordinate cannot be projected to a plane by the given ILcdProjection, a TLcdOutOfBoundsException is thrown.
The interface ILcdProjection has several methods that define the valid area of a map projection. The method inLonLatBounds checks whether a given lon-lat-height coordinate is inside the valid area of the ILcdProjection. The methods boundaryLons(aLatitude) and boundaryLats(aLongitude) determine the valid longitude and latitude intervals, respectively, for a given latitude or a given longitude. The inverse
transformation of an ILcdProjection also has a valid domain. The methods inWorldBoundsOnSphere and inWorldBoundsOnEllipsoid check whether a given Cartesian coordinate is inside the domain of the inverse transformation for a sphere and an ellipsoid,
respectively.
Classes implementing the interface ILcdProjection provide transformations for both spherical and ellipsoidal models of the earth. If the ellipsoidal formulas are not useful
or not available, you can approximate the ellipsoidal methods by the spherical methods using the semi-major axis as the earth
radius.
Each ILcdProjection has a point of origin. The point of origin is the geodetic coordinate that corresponds to the origin of the planar Cartesian coordinate system.
How this point of origin is specified or how it can be set, depends on the characteristics of the ILcdProjection and is specified by the classes implementing the interface ILcdProjection. In addition to the projection origin, an ILcdProjection has other properties depending on the type of ILcdProjection as described in Extensions of ILcdProjection.
The interface ILcdProjection applies the Listener pattern in collaboration with java.beans.PropertyChangeListener. A PropertyChangeListener accepts java.beans.PropertyChangedEvent objects from the ILcdProjection objects to which it is registered. A PropertyChangeEvent is sent from an ILcdProjection to its listeners whenever one of its properties has changed.
For more information on listening to changes, refer to Notifying objects of changes with listeners.
Extensions of ILcdProjection
The interface ILcdProjection is further extended in several interfaces. This is done through a classification of the projections according to their properties.
-
ILcdCylindricalspecifies a cylindricalILcdProjection. It is defined by wrapping a cylinder around the earth globe such that it touches the equator. The point of origin of theILcdProjectionis always located on the equator and is only determined by the longitude.
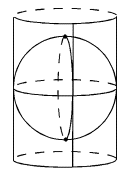
-
ILcdTransverseCylindricalspecifies a transverse cylindricalILcdProjection. It is defined by a cylinder that touches the earth globe at the poles. The point of origin of theILcdProjectionis defined by the central meridian and is always located on the equator.
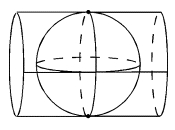
-
ILcdObliqueCylindricalspecifies a cylindricalILcdProjectionwith the cylinder tilted over an azimuth angle.
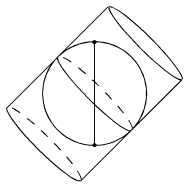
-
ILcdAzimuthalspecifies an azimuthalILcdProjection. It is defined by a tangent plane at the point of origin defined by a geodetic latitude and longitude.
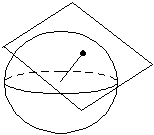
-
ILcdConicspecifies a conicalILcdProjectionthat cuts the earth globe at two standard parallels and for which the point of origin of theILcdProjectionis defined by a geodetic latitude and longitude.
-
ILcdPerspectiveis an extension ofILcdAzimuthal, where the point of origin is not necessarily located on the surface of the earth.
For a complete list of available sub-interfaces, refer to the package projection
in the API reference.
Main implementations of ILcdProjection
LuciadLightspeed provides implementations for commonly used projections. All implementations extend abstract adapter classes
for the interfaces defined in Extensions of ILcdProjection. These abstract classes implement the properties specific for each type of ILcdProjection. They also have a method loadProperties to initialize instances of each class.
TLcdProjectionFactory creates ILcdProjection objects using this properties mechanism.
-
TLcdEquidistantCylindricalimplements the interfaceILcdCylindrical. It transforms the lon-lat coordinates to a planar representation by considering longitude and latitude as simple rectangular coordinates. It is often used as a grid system for basic unprojected geodetic coordinates. -
TLcdMercatorimplements the interfaceILcdCylindrical. It is used for world maps and maritime navigational charts. It is also used for grid systems for maritime navigational raster data such as the British Admiralty charts. -
TLcdTransverseMercatorimplements the interfaceILcdTransverseCylindrical. It is the basis for the UTM grid system (TLcdUTMGridandTLcdUTMGridSystem). -
TLcdLambertConformalimplements the interfaceILcdConic. It is used for aeronautical navigational charts. It is also the basis for a number of national grid systems, for example,TLcdLambert1972BelgiumGridReferenceandTLcdLambertFrenchGridReference. -
TLcdStereographicimplements the interfaceILcdAzimuthal. It is used for aeronautical operational display systems such as an Air Track Display. It is also the basis for a number of national grid systems such asTLcdRD1918DutchGridReference. -
TLcdGnomonicimplements the interfaceILcdAzimuthal. It is used for maritime operational display systems. -
TLcdOrthographicimplements the interfaceILcdAzimuthal. -
TLcdVerticalPerspectiveimplements the interfaceILcdPerspective. It is typically used for interpreting satellite images. -
TLcdObliqueMercatorimplements the interfaceILcdObliqueCylindrical. -
TLcdCassiniimplements the interfaceILcdTransverseCylindrical. -
TLcdPolarStereographicimplements the interfaceILcdAzimuthal, used for mapping polar areas. It is also used to define the UTM grid system for polar areas.
For a detailed description of the available implementations of the interface ILcdProjection, refer to the package projection in the API reference.
Literature on map projections
-
Snyder, Map Projections: A Working Manual, 1987.
-
Bugayevskiy, Snyder, Map Projections : A Reference Manual, 1995.
-
Snyder, Flattening the Earth : Two Thousand Years of Map Projections, 1997.
-
Pearson, Map Projections : Theory and Applications, 1990.
-
Maling, Coordinate systems and map projections, 1992.