-
public interface ILcdIntersectionMatrixPatternThis interface defines a topological relationship between two shapes by imposing conditions on the intersection matrix of the two shapes.- Since:
- 10.0
- See Also:
ILcdIntersectionMatrix
-
-
Field Summary
Fields Modifier and Type Field and Description static ILcdIntersectionMatrixPatternCONTAINSMatrix pattern checking the topological relationship contains.static ILcdIntersectionMatrixPatternCOVERED_BYMatrix pattern checking the topological relationship coveredBy.static ILcdIntersectionMatrixPatternCOVERSMatrix pattern checking the topological relationship covers.static ILcdIntersectionMatrixPatternCROSSESMatrix pattern checking the topological relationship crosses.static ILcdIntersectionMatrixPatternDISJOINTMatrix pattern checking the topological relationship disjoint.static ILcdIntersectionMatrixPatternEQUALSMatrix pattern checking the topological relationship equals.static ILcdIntersectionMatrixPatternINTERSECTSMatrix pattern checking the topological relationship intersects.static ILcdIntersectionMatrixPatternOVERLAPSMatrix pattern checking the topological relationship overlaps.static ILcdIntersectionMatrixPatternTOUCHESMatrix pattern checking the topological relationship touches.static ILcdIntersectionMatrixPatternWITHINMatrix pattern checking the topological relationship within.
-
Method Summary
All Methods Instance Methods Abstract Methods Modifier and Type Method and Description booleanmatches(ILcdIntersectionMatrix aIntersectionMatrix)Checks whether the topological relationship defined by this matrix pattern holds for the given intersection matrix.
-
-
-
Field Detail
-
DISJOINT
static final ILcdIntersectionMatrixPattern DISJOINT
Matrix pattern checking the topological relationship disjoint. Two shapes are disjoint if they have no points in common. This relation is the negation of the
INTERSECTSrelation.
In terms of the DE-9IM matrix, this relation is true in case the intersection matrix matches one of the following patterns: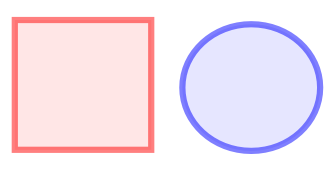
In the example in the image, the red and blue shape are disjoint. FF*FF****
-
INTERSECTS
static final ILcdIntersectionMatrixPattern INTERSECTS
Matrix pattern checking the topological relationship intersects. Two shapes intersect if they have at least one point in common. This relation is the negation of the
DISJOINTrelation.
In terms of the DE-9IM matrix, this relation is true in case the intersection matrix matches one of the following patterns: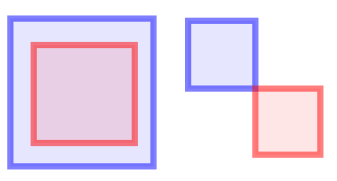
In the two examples in the image, the red and blue shapes intersect. T*********T**********T*********T****
-
CONTAINS
static final ILcdIntersectionMatrixPattern CONTAINS
Matrix pattern checking the topological relationship contains. This relation is the inverse of the
WITHINrelation. The first shape contains the second shape if the following conditions are fulfilled:- their interiors intersect
- the exterior of the first shape does not intersect the interior nor the boundary of the second shape
Note that the first condition implies that a polygon does not contain its own contour (a closed polyline). This illustrates the subtle difference between the contains relation and the
COVERSrelation , since a polygon covers its own contour.
In terms of the DE-9IM matrix, this relation is true in case the intersection matrix matches one of the following patterns: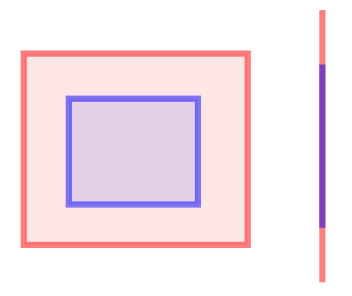
In the two examples in the image, the red shape contains the blue shape. T*****FF*
-
WITHIN
static final ILcdIntersectionMatrixPattern WITHIN
Matrix pattern checking the topological relationship within. This relation is the inverse of the
CONTAINSrelation. The first shape is within the second shape if the following conditions are fulfilled:- their interiors intersect
- the exterior of the second shape does not intersect the interior nor the boundary of the first shape
Note that the first condition implies that the contour of a polygon is not within the polygon. This illustrates the subtle difference between the within relation and the
COVERED_BYrelation, since the contour of a polygon is covered by the polygon.
In terms of the DE-9IM matrix, this relation is true in case the intersection matrix matches one of the following patterns: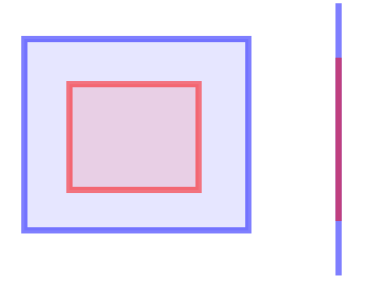
In the two examples in the image, the red shape is within the blue shape. T*F**F***
-
COVERS
static final ILcdIntersectionMatrixPattern COVERS
Matrix pattern checking the topological relationship covers. This relation is the inverse of the
COVERED_BYrelation. The first shape covers the second shape if the following conditions are fulfilled:- both shapes intersect
- the exterior of the first shape does not intersect the interior nor the boundary of the second shape
Note the subtle difference with the
CONTAINSrelation.
In terms of the DE-9IM matrix, this relation is true in case the intersection matrix matches one of the following patterns: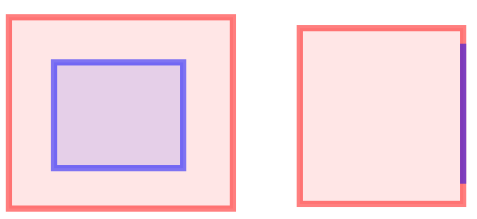
In the two examples in the image, the red shape covers the blue shape. T*****FF**T****FF****T**FF*****T*FF*
-
COVERED_BY
static final ILcdIntersectionMatrixPattern COVERED_BY
Matrix pattern checking the topological relationship coveredBy. This relation is the inverse of the
COVERSrelation. The first shape is covered by the second shape if the following conditions are fulfilled:- both shapes intersect
- the exterior of the second shape does not intersect the interior nor the boundary of the first shape
Note the subtle difference with the
WITHINrelation.
In terms of the DE-9IM matrix, this relation is true in case the intersection matrix matches one of the following patterns: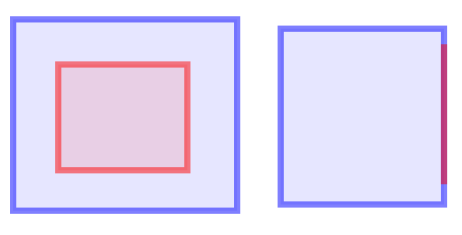
In the two examples in the image, the red shape is covered by the blue shape. T*F**F****TF**F*****FT*F*****F*TF***
-
TOUCHES
static final ILcdIntersectionMatrixPattern TOUCHES
Matrix pattern checking the topological relationship touches. Two shapes touch each other if the following two conditions are fulfilled:
- their interiors have no point in common
- the boundary of one of the two shapes has at least one point in common with the other shape
In terms of the DE-9IM matrix, this relation is true in case the intersection matrix matches one of the following patterns: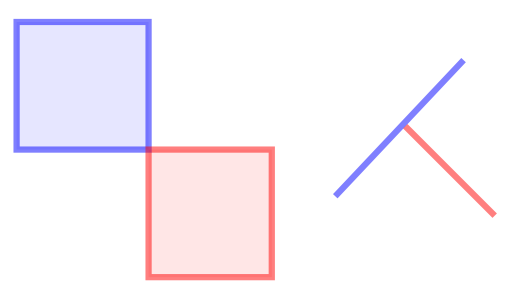
In the two examples in the image, the red and blue shapes touch. FT*******F**T*****F***T****
-
CROSSES
static final ILcdIntersectionMatrixPattern CROSSES
Matrix pattern checking the topological relationship crosses. Two shapes cross each other if the following three conditions are fulfilled:
- their interiors have at least one point in common
- the dimension of the intersection of their interiors is smaller than the dimension of the interior of the shape with the highest dimension
- neither shape lies completely inside the other shape
In practice, this means that:
- Two 1-dimensional shapes (such as polylines) cross if the intersection of their interiors has dimension 0.
- A 1-dimensional shape crosses a 2-dimensional shape if the interior of the 1-dimensional shape intersects both the interior and exterior of the 2-dimensional shape.
- A 0-dimensional shape (such as a point) never crosses another shape.
- Two 2-dimensional shapes never cross each other.
In terms of the DE-9IM matrix, this relation is true in case the intersection matrix matches one of the following patterns: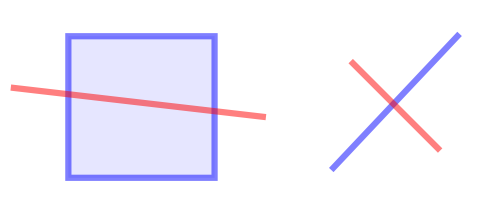
In the two examples in the image, the red and blue shapes cross. 0********for two 1-dimensional shapesT*T******for a 1-dimensional and a 2-dimensional shapeT*****T**for a 2-dimensional and a 1-dimensional shape
-
OVERLAPS
static final ILcdIntersectionMatrixPattern OVERLAPS
Matrix pattern checking the topological relationship overlaps. Two shapes overlap if the following conditions are fulfilled:
- their dimension is the same
- the intersection of their interiors has the same dimension as the shapes
- neither shape lies completely inside the other shape
This means that the overlap relation is always false for a:
- 0-dimensional shape (such as a point) and any other shape
- 1-dimensional shape and a 2-dimensional shape
In terms of the DE-9IM matrix, this relation is true in case the intersection matrix matches one of the following patterns: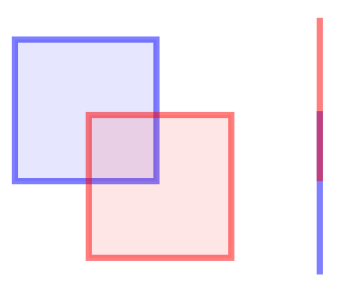
In the two examples in the image, the red and blue shapes overlap. 1*T***T**for two 1-dimensional shapesT*T***T**for two 2-dimensional shapes
-
EQUALS
static final ILcdIntersectionMatrixPattern EQUALS
Matrix pattern checking the topological relationship equals. The equals relation is true for two shapes which have the same interior, boundary, and exterior.
In terms of the DE-9IM matrix, this relation is true in case the intersection matrix matches one of the following patterns:
In the example in the image, the red and blue shape are equal. T*F**FFF*
-
-
Method Detail
-
matches
boolean matches(ILcdIntersectionMatrix aIntersectionMatrix)
Checks whether the topological relationship defined by this matrix pattern holds for the given intersection matrix.- Parameters:
aIntersectionMatrix- the intersection matrix- Returns:
trueif the binary topology relation defined by this matrix pattern holds foraIntersectionMatrix, false otherwise.
-
-